What i’ve been thinking about
This post will largely be a recap of the past month of trying to resolve a clearer picture of my research direction for the remainder of the scholar’s program.
The motivating question behind my research thus far is whether or not it possible to make more optimal use of the compute resources available at test time in order to refine the output produced by a machine learning model. To rephrase:
If we’re being clever can we create constructions such that smaller adaptive models can instead leverage test time compute to overcome the handicap of having a smaller number of learnable parameters?
For deep learning models there seems exists an asymmetry between training and inference (test time) compute. State of the art models are typically trained with large compute budgets and subsequently deployed on machines which use significantly smaller computational resources. Does this represent an inefficient underutilization of computation? Put succinctly: are there ways to remedy the asymmetry of training vs test compute?
Anthropomorphically, I think there’s good motivation here. After all, given more time to think, humans generally tend to produce higher quality answers- perhaps by spending those additional cognitive resources on resolving ambiguity.
There are a number of particularly interesting approaches to this problem some of which i’ve talked about or hinted at in previous posts. Given the short time constraints of the scholar’s research program however, I think it makes sense to limit the scope of this investigation to just two potential avenues , namely the effects of adding in temporal recurrence into fast autoregressive transformers, and the effect of adding externalized memory into existing models. The general idea here is that maybe the addition of temporal recurrence will enable training of transformer models which can iteratively refine their outputs (at least in language modeling contexts) while simultaneously decreasing sampling complexity and alleviating the per parameter computational cost increases seen in typical depth-wise recurrent architectures.
A detour into city paths
Both as a mechanism for investigating test time compute, and as a “fail fast” test i’ve constructed a dataset that’s turned out to be surprising in a number of ways. For now what i’m just calling “The City Dataset” (Github link forthcoming I swear) was made by constructing a DAG from publicly available data about US population centers. It includes some basic demographic information as well as GPS coordinates for almost 30,000 distinct cities and municipalities distributed across the nation. Besides serving as a traversable knowledge graph, this DAG allows us to also construct simpler smaller datasets.
Particularly, one of these derivative datasets is the “Shortest Path Dataset” (SPD). SPD is constructed using the coordinates found in the City Dataset and uses Dijkstra’s to enumerates several million “shortest paths” between pairs of US cities. I treat this a sequence modeling task using a scheme akin to traditional language modeling where the network is asked to given a sequence of inputs and asked at each timestep to predict the next token (city) in the sequence target. A RNN was constructed as baseline (from which we could later compare other models trained with similar levels of compute but utilizing increased compute at test time).
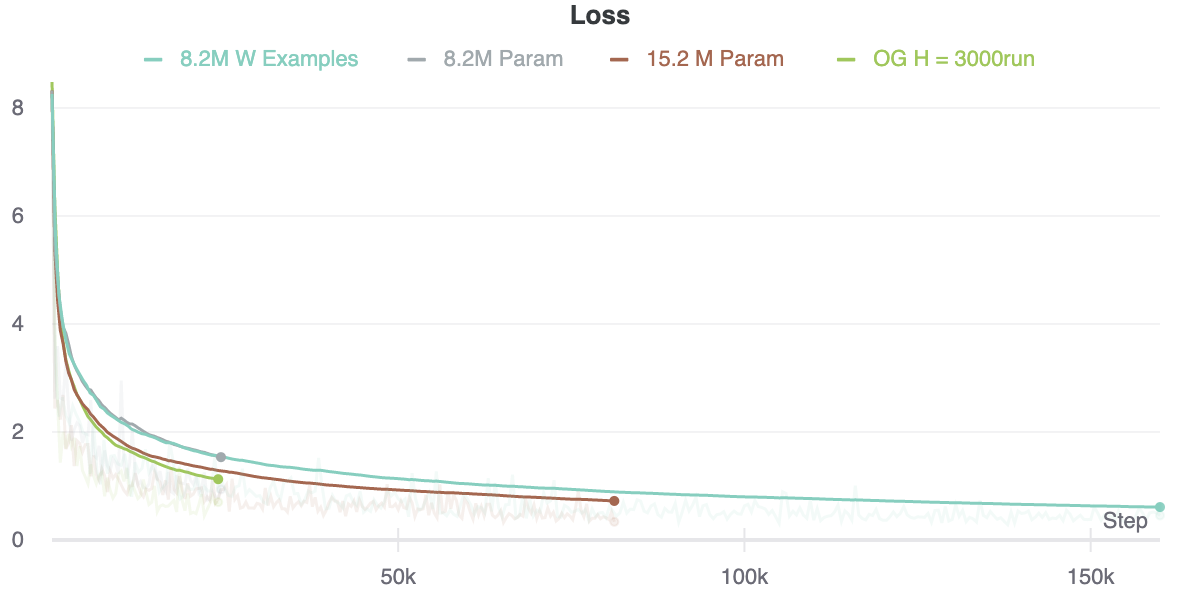
Above, I plot performance for different sized architectures. Notice that training loss tends to bottom out on the order 0.3~0.4. Because cross entropy loss isn’t a particularly useful metric in this case I constructed other metrics that measure the performance of the model along certain axes. Namely:
- Do the generated output paths lack illegal jumps? Here Illegal jumps are defined as jumps between two cities that are over the “connected distance” used to generate the DAG - the distance below which we consider two cities to be connected.
- Is the length of the total path traversed by the generated output bounded? In other words, this metric checks to ensure that even if we don’t generate the exact optimal path, the path that we do generate deviates from the optimal path only by a small amount.
- Does the generated output actually end in the same city as the optimal path?
What’s remarkable is that even with a somewhat decent training loss, performance with regard to the these other metrics is abysmal. It’s still a bit early to say definitively but as far as I can tell, even with low NLL loss generating a sample output that satisfies even one of these metrics is exceedingly, exceptionally rare.
Despite it’s artificiality, it’s important to remember it’s not actually solving this particular task itself I care about. What was important here was finding a domain that was sufficiently challenging where the benefits of leveraging compute at test time would be clear. Shortest Path seems attractive because any traditional single pass architecture should be algorithmically bounded in how well it should perform on this. Additionally, as an example of test time compute it’s easy to imagine a model that first generates a path that’s directionally correct and then continually refines its output. What’s a bit surprising about this task is how difficult its actually proven to be even with respect to generating just decently-performing baselines.
To be continued
There’s quite a bit going through my head currently. I’m devising better means to instrument what’s going on with this dataset as well as mechanisms to actually extract performance with increases in test time compute from other models using other paradigms. Above all, while i’m bullish on the idea of test time compute, I still have deep doubts about the kludgyness and crudity of my methods. I would like to leave you with something more cogent, more coherent, and more insightful but for now i’m stumbling around in the darkness. Anyway, that’s it for now. Catch you on the flip.