One of the particularly fascinating things i’ve encountered during NEURIPS 2020 was a workshop on deep implicit layers that raises some questions about the nature of my current project proposal for the OpenAI scholars program. While I highly recommend checking out the tutorial and working through the main ideas for yourself, I’ll try to super briefly outline the principle argument and method. All figures in this post are stolen from their work.
Deep equilibrium models are built on top 3 ideas.
- Implicit layers are more expressive than explicit layers. That is, instead of having layers that express how to calculate a model’s output from its input we can instead specify which conditions we would like for a model’s output and input to jointly satisfy. This has a number of attractive properties (all worthy of an entire blog post) but prime among them is the nice property of decoupling a model’s solution from the procedure that generates it.
- Feedforward models can be represented by an equivalent, weight-tied, recurrent back-propagation model which they call a deep equilibrium model.
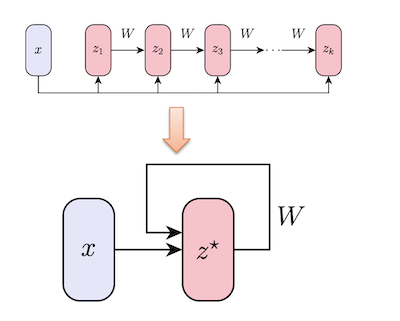
- Deep equilibrium models can be constructed such that they converge to a fixed point. What’s particularly dope is that this property combined with the decoupling property talked about above ultimately lets you plug in your models dynamics into any black box optimizer.
The upshot, is that the implicit function theorem gives a really nice way of computing gradients near fixed points without having to store the usual intermediaries you would if you were computing and storing the computational graph using standard auto-differentiation. This allows for some fairly massive reductions in the memory requirements for equivalently sized models. What’s interesting is to measure the performance of DEQ models when compared to more traditional single pass feed forward models.
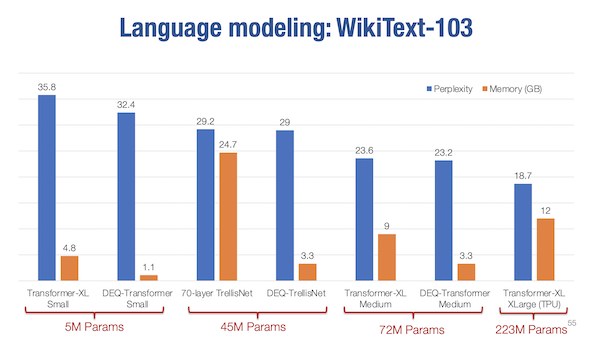
In some sense these deep equilibrium models can be thought of as deep networks with infinite depth since they’re iteratively evaluated until their output reaches convergence up to some tolerance threshold. The troubling question this raises for the research and my project proposal research is whether a DEQ represents the limits of what’s possible vis-à-vis iterative refinement. To rephrase, if the principal idea in my work is that it may be possible to continually and iteratively improve performance of smaller models by more optimally leveraging test time compute, then the fixed point of DEQ models may represent the upper bound of iterative application.
To be sure, even if DEQs do represent some performance limit for fixed parameter models there still exist fascinating questions to be asked here nonetheless. Why are the performances gains so marginal? How does the performance of DEQ models change with task algorithmic complexity? etc, etc…
To be honest, I’m still not sure how to grapple with any of these issues, or whether these are signs that perhaps I should consider alternative proposals. For now, my two pronged approach is as follows
-
Fail Fast Tests: Make these questions more concrete by examining the performance of recursive transformers and external memory models on tasks we believe test time compute will actually make a difference. Thus far i’ve constructed a set of simple algorithmic tasks (i’ll soon make these available on github). The motivation here is to quickly gauge for signs of life in this work.
-
Explore EBM backup plan As far as I can tell, test time compute paradigm actually seems to be more at home in the energy based model framework where the idea is that you characterize an energy function that parametrizes the correspondence between your input and output. At inference, you then search for an output that minimizes the energy function (using gradient descent if the latent space is continuous) using any standard optimization technique of choice. Consequently, as a backup I’m also reviewing the EBM literature to build familiarity with this space.
Anywho that’s enough rambling for now. Catch you on the flip.